author

koly

| 6,086 words | haskell

haskell中的applicative和Monads

写本文的目的是为了好好理解一下Haskell中的Monads。本文基于《Learn You a Haskell for Great Good》。了解Monads，首先要了解Type Class, the Functor Type Class, Applicative Functors。咱们一个一个慢慢来。

Type Class

这个比较简单，类似Java语言中的Interface。也就是说Haskell中，通过type class可以定义一种行为。所谓行为，就是接收一个东西，然后输出一个特定的东西。正如函数所做的那样。

为了创造一个Type Class，我们需要什么？

总得有个名字吧。然后得定义一个行为。这里行为怎么定义呢？行为通过函数来表示，所以定义行为就等于定义函数。既然是函数，自然有函数名，输入，输出。

编译器怎么知道你是在创建Type Class呢？关键字来了。这里有两个关键字：class和where。

来个例子：

1
2
3
4
5
class Eq a where
  (==) :: a -> a -> Bool
  (/=) :: a -> a -> Bool
  x == y = not (x /= y)
  x /= y = not (x == y)

上面这个例子中，“Eq”表示该Type Class的名字。“a”是Type Parameter，表示任意一种类型，如Int, String等。之后（第二行和第三行）是定义了两个方法“==”和“/=”，使用括号将他们括起来表示他们是中缀，也就是说使用的时候要么是“5 == 4”或者是“(==) 5 4”。之后使用“::”来定义方法的输入和输出类型，两个函数都是接收两个类型为“a”的输入，输出一个Bool型。定义之后是方法的两个默认实现，由于两个实现彼此依赖，所以实现的时候只需要实现其中一个，另一个使用默认的就可以了。

来看一个实现:

1
2
3
4
5
6
7
8
9
--定义TrafficLight
data TrafficLight = Red | Yellow | Green

--实现Eq type class
instance Eq TrafficLight where
  Red == Red = True
  Yellow == Yellow = True
  Green == Green = True
  _ == _ = False

上例中首先定义了一个TrafficLight类，该类有三个可取值，分别为：Red, Yellow和Green。之后使用“instance”来实现“Eq” type class。也就是说给“TrafficLight”类加上“==”和“/=”这两个行为。实现中，只实现了“==”方法，根据上面的介绍，“/=”使用了默认实现。现在，我们可以看看Red == Yellow，Red == Red的值了。

至此，我们知道了Type Class是什么，如何定义，及如何使用。接下来是Functor Type Class。

Functor Type Class

首先，这是一个Type Class。是Haskell定义的众多Type Class中的一个。

我们来看看Functor Type Class的定义：

1
2
class Functor f where
  fmap :: (a->b) -> f a -> f b

首先，这个Type class的名字叫Functor。其次，它定义了一种行为，称为fmap。该行为接收一个函数及“f a”返回一个“f b”，其中a和b是接收的函数的输入和输出。“f a”和“f b”是两种类型，而“f”称为type constructor，就是说“f”接收一个类型，返回一个新的类型。举个例子：

1
2
3
instance Functor Maybe where
  fmap f Nothing = Nothing
  fmap f (Just x) = Just (f x)

我们与上面Functor的定义对应一下：Maybe就是上面的f，则fmap的定义变成了fmap :: (a->b) -> Maybe a -> Maybe b。如何应用呢？首先，由于Maybe这个type constructor实现了Functor，那么就可以在由Maybe建立的类型上使用fmap函数，该函数接收一个a->b的函数以及一个Maybe a，返回一个Maybe b。假设a->b是(+3)，此处(+3)的定义为Num a => a -> a。此时，还需要另一个Maybe a类型的参数，假设为Maybe Int，则调用为fmap (+3) (Just 3)，得到Just 6。针对这个例子，翻译一下fmap :: (a->b) -> Maybe a -> Maybe b，则为fmap :: (Int -> Int) -> Maybe Int -> Maybe Int。

回顾一下整个过程：

  • 首先根据fmap :: (a->b)->f a->f b，确认f，f必须为type constructor。比如Maybe
  • 之后确认fmap接收的函数参数(a->b)，比如(Int -> Int)
  • 然后确认fmap接收的第二个参数f a，由于第一步已经确认了f，第二步确认了a，所以这里就好确定了。比如为Maybe Int。

我们再来分析一下fmap干了什么事情？以fmap (+3) (Just 3)为例，fmap将(+3)这个函数应用于(Just 3)中的值3，得到结果6，然后将6转换为Maybe Int型，即Just 6。如果将fmap这个名字拆为f和map，并对f和map分别理解，会怎么样呢？

对map，它表示了一种转换。先来看看haskell中的map函数：(a -> b) -> [a] -> [b]。map函数接收一个函数以及一个数组，然后对数组中的每一个值应用该函数，然后将得到的结果放在一个数组中。简单来说就是将数组a转换为数组b。

fmap中的map，表示的也是一种转换。而f，则可以理解为一种context（域），或者是一种盒子。fmap做得事情就是将盒子中的值拿出来，应用转换函数，然后将结果再放回盒子中。此盒子有一个构造函数，输入为值，输出为盒子。比如Maybe，输入Int，则输出的盒子为Maybe Int。adit.io有一个很好的图：

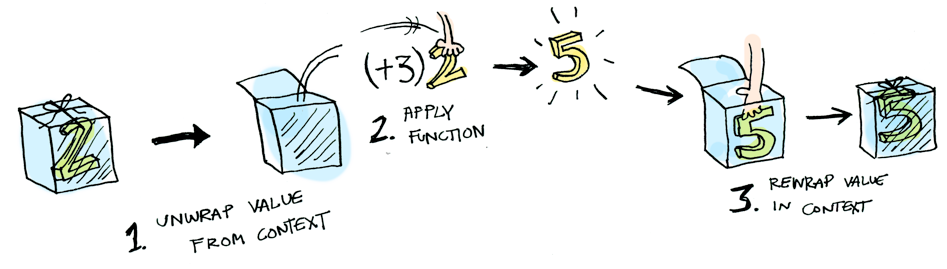
functor

我们再来看看数组:

1
2
instance Functor [] where
  fmap = map

首先[]是一个type constructor，输入一种类型，得到另一种类型。比如输入Int，得到[Int]。fmap = map，为什么呢？正常的fmap是将f替换为[]为fmap :: (a->b)->[a]->[b]，同map的定义一致。所以对[]，map就是fmap。

fmap也可以这样表述：fmap接收一个函数以及一个Functor，然后输出一个新的Functor，同样一个来自adit.io的图：

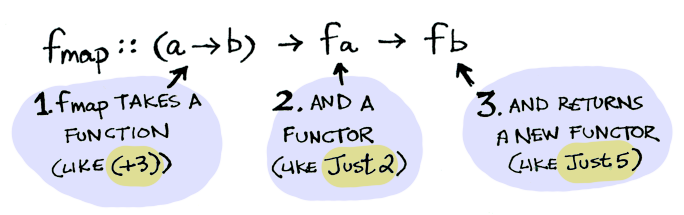
function_def

Functor就是指一个通过Type Constructor得到的具体类型，而该Type Constructor实现了Functor type class。比如Just 3是根据Maybe得到的具体类型，而Maybe实现了Functor type class，则Just 3就是一个Functor。fmap (+3) (Just 3)得到Just 5，Just 3是一个Functor，Just 5是另一个Functor。

简单一点，Functor是一个Type Class，其定义了一种行为叫fmap，fmap接收一个函数和一个functor，得到一个新的functor。

Applicative Type Class

Applicative 也是一个Type Class。

先不提Applicative type class。我们先来看看Functor：

1
2
class Functor f where
  fmap :: (a->b) -> f a -> f b

Functor可以让我们这样:

1
fmap (+3) (Just 3) -- the result is Just 6

如果是下面这样，输出的是什么呢？

1
fmap (+) (Just 3) -- what's the result?

直接在ghci中输出的话，ghci会告诉你找不到对应的show方法。如果使用:t fmap (+) (Just 3)，结果是Num a => Maybe (a -> a)。这是一种具体类型(concrete type)。考虑到Maybe的定义:

1
data Maybe a = Nothing | Just a

则“Maybe (a -> a)”对应的是“Maybe (a->a) = Nothing | Just (a->a)”，因此它的一个实例为“Just (\x->x)”。

对于“(a->a)”，我们可以看看下面这段代码：

1
2
3
4
5
applyFunc2Value :: [(a->b)] -> a -> [b]
applyFunc2Value [] _ = []
applyFunc2Value (x:xs) y = x y : (applyFunc2Value xs y)

applyFunc2Value [(*3), (+2), (\x->x+10)] 4 -- result is: [12,6,14]

上例中的“[(a->b)]”是一个具体类型，而[]于Maybe类似，所以“Maybe (a->b)”也是一个基本类型。

1
2
3
4
5
addMaybe :: Maybe (a->b) -> a -> Maybe b
addMaybe Nothing _ = Nothing
addMaybe (Just f) x = Just (f x)

addMaybe (Just (+3)) 5 -- result is: Just 8

至此，我们知道“Maybe (a->b)”是一种具体类型，以及可以如何使用它。

Functor中的fmap接收一个函数和一个functor，得到另一个functor，比如: fmap (+3) (Just 5)会得到Just 8。如果我们想要计算Just (+3)与Just 8的值，就无法使用Functor中的fmap。而这时，applicative就派上用场了。

先看看applicative type class的定义：

1
2
3
class (Functor f) => Applicative f where
  pure :: a -> f a
  (<*>) :: f (a->b) -> f a -> f b

首先，Applicative的instance是一个Functor，即上面的f是一个Functor，也就是说有instance Functor f where ...。其次，Applicative type class定义了两个行为，也就是两个函数。一个是pure，另一个是“<*>”。pure函数接收一个参数，然后通过f来创建一个新的实例。如果f为Maybe，则pure可以为：pure x = Just x。“<*>”函数接收一个函数Functor和一个Functor，返回一个Functor。比如(Just (+3)) <*> (Just5)得到Just 8。这样就可以计算上述的Just (+3)与Just 8的值了。

按照盒子的比喻，<\*>是将第一个盒子中的函数拿出来，应用到第二个盒子中的值，然后将结果放回盒子中。这里参数中的两个盒子和返回值的盒子都是一样的。adit.io中的图：

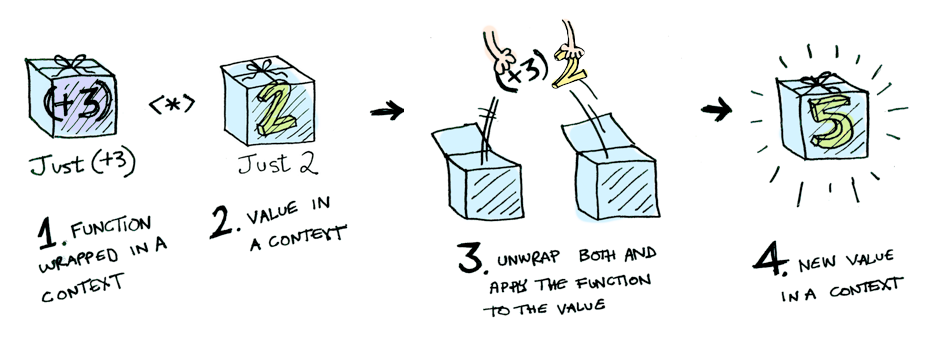
applicative just

先来看一个例子：

1
2
3
4
5
6
7
-- Maybe 实现Applicative
instance Applicative Maybe where
  pure = Just
  Nothing <*> _ = Nothing
  (Just f) <*> something = fmap f something

pure (+3) <*> Just 10

除了上面的用法，我们还可以：

1
pure (+) <*> Just 3 <*> Just 5

这就是pure f <*> x <*> y...，根据定义有：pure f <*> x = fmap f x，所以pure f <*> x <*> y可以写成fmap f x <*> y，在Control.Appicative中，定义了：

1
2
(<$>) :: (Functor f) => (a->b) -> f b -> f b
f <$> x = fmap f x

所以fmap f x <*> y可以写成f <$> x <*> y，比如：(+) <$> Just 3 <*> Just 5即为fmap (+) (Just 3) <*> Just 8。

对于[]，有:

1
2
3
4
5
6
7
8
instance Applicative [] where
  pure x = [x]
  fs <*> xs = [f x | f <- fs, x <- xs]

pure "hey" :: [String]
[(*0), (+100), (^2)] <*> [1,2,3]
[(+), (*)] <*> [1,2] <*> [3,4]
(++) <$> ["ha", "heh", "hmm"] <*> ["?", "!", "."]

对于函数，有：

1
2
3
4
5
6
7

instance Applicative ((->)r) where
  pure x = (\_ -> x)
  f <*> g = \x -> f x (g x)

(+) <$> (+3) <*> (*100) $ 5
(\x y z -> [x,y,z]) <$> (+3) <*> (*2) <*> (/2) $ 5

Monads

在介绍Monads之前，我们先来回顾一下Functor和Applicative。

  • Functor和Applicative都是type class
  • Functor的fmap函数是接收一个函数，和一个盒子，将函数应用于盒子里的值，得到的结果放在盒子里。fmap :: (a->b) -> f a -> f b
  • Applicative的<*>函数是接收一个里面是函数的盒子及一个里面是数值的盒子，将函数应用于数值，然后将结果放回盒子里。(<*>) :: f (a->b) -> f a -> f b

而Monad呢？

  • Monad中“>>=”函数的定义：(>>=) :: (Monad m) => m a -> (a -> m b) -> m b
  • Monad的(>>=)函数接收一个盒子及一个可将数值转换为盒子的函数，将函数应用于盒子里的值，得到的盒子就是(>>=)函数的返回。其中(>>=)称为bind

如你所料，Maybe也是一个Monad。先来看看怎么用：

1
Just 9 >>= (\x -> return (x*10)) --result is: Just 90

“>>=”的左边是一个盒子，右边是一个函数，该函数接收一个值，返回一个盒子，该盒子就是“>>=”的返回值。

知道了怎么用，来看看Monad的完整定义：

1
2
3
4
5
6
7
8
9
10
class Monad m where
  return :: a -> m a

  (>>=) :: m a -> (a -> m b) -> m b

  (>>) :: m a -> m b -> m b
  x >> y = x >>= \_ -> y

  fail :: String -> m a
  fail msg = error msg

定义中的第一个函数与Applicative中的pure类似，将一个值转为Monad，承担了转换作用。
第二个函数“>>=”上面已经介绍了。第三个函数“>>”接收两个Monad，然后返回第二个Monad。最后一个“fail”函数，定义了失败时候的行为，一般我们都不用管它。

再来看看Maybe对Monad的实现：

1
2
3
4
5
instance Monad Maybe where
  return x = Just x
  Nothing >>= f = Nothing
  Just x >>= f = f x
  fail _ = Nothing

于是我们可以：

1
2
3
return "hello" :: Maybe String
Just 3 >>= (\x->return $ x + 9)
Just 3 >> Nothing

由于“>>=”函数的第二个参数接收一个盒子，返回一个盒子。所以可以链式使用该函数。举个例子：

1
2
3
4
add9 :: Int -> Maybe Int
add9 x = if x < 0 then Nothing else Just (x+9)

Just 3 >>= add9 >>= add9 >>= add9

简单来说，Monad就是代表了一种行为，这种行为根据一个盒子和一个返回盒子的函数，来产生另一个盒子，借用adit.io的图：

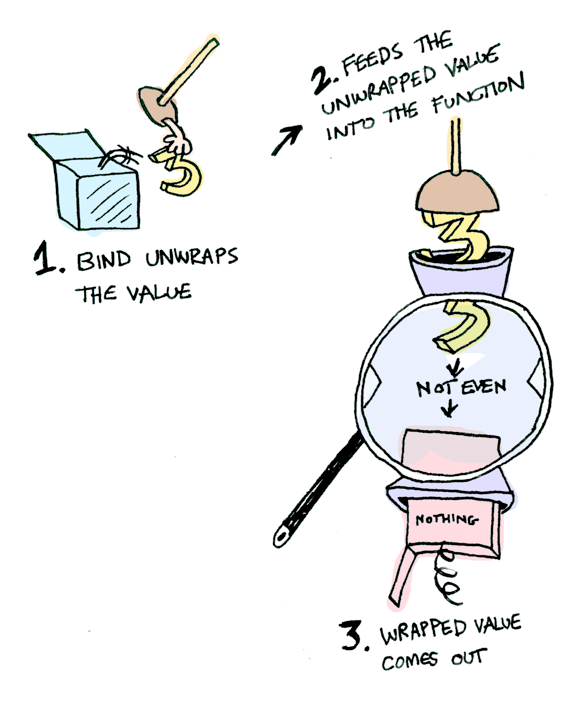
monad just

总结

在Haskell里面，有一些基本类型，比如Int, Double, String。对于这些类型，有一些操作，比如: +，-，*。这些简单类型可以完成一些运算，但是在遇到比较大的问题的时候，由于代码增多，就需要更高级的、抽象的类型来使程序更好编写，更易阅读，更易维护。于是，高级类型就出现了，比如表示不确定性的Maybe，表示列表的[]，表示输入输出的IO。对于这些类型，我们也需要一些操作，比如对Maybe 7 + Maybe 8，我们希望得到Maybe 15。所以，我们定义了一些type class，将通用的行为抽象并定义为具体的type class。通过这些type class，我们可以在操作高级类型的时候重用基本类型的操作。比如Maybe 7 + Maybe 8 = Maybe (7+8)。于是，有了这些抽象：

  • 高级类型由初级类型组建，只是加上了一些context。我们将高级类型类比为盒子，盒子里面装有基本类型，它可以是函数，也可以是数值
  • 有了盒子之后，我们发现我们常常需要盒子与盒子的操作，以及盒子与非盒子的操作，非盒子包括了函数和数值，比如Maybe是一个盒子，那么有(*3)与Just 3的操作，也需要Just (*3)与Just 3的操作。也需要Just 3与(\x->Just (x+3))的操作。
  • 函数与盒子的操作，我们定义了Functor
  • 盒子与盒子的操作，我们定义了Applicative
  • 盒子与返回盒子的函数的操作，我们定义了Monad

借用adit.io的图：

recap

以及总结：

  • functors: you apply a function to a wrapped value using fmap or <$>
  • applicatives: you apply a wrapped function to a wrapped value using <*> or liftA
  • monads: you apply a function that returns a wrapped value, to a wrapped value using >>= or liftM

参考资料

[1] 《Learn You a Haskell for Great Good》
[2] http://adit.io/posts/2013-04-17-functors,_applicatives,_and_monads_in_pictures.html